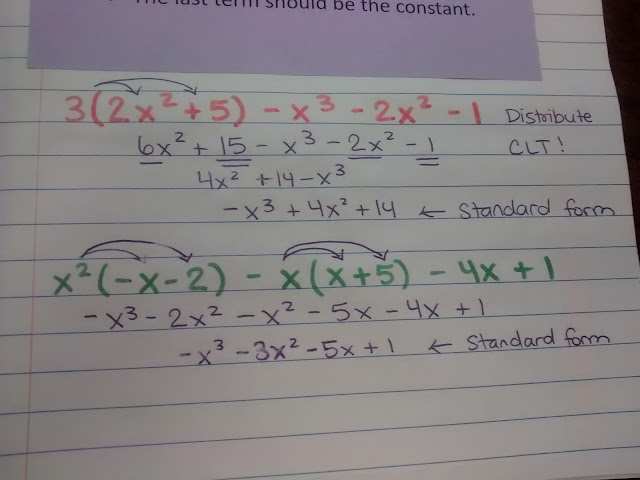Quantcast
Channel: Math = Love
Viewing all 1077 articles
Browse latest View live
↧

Algebra 2 Exponent Rule Review

October 5, 2015, 5:30 am
$
0
0
Every year, I keep trying a different way to review exponent rules.  For my Algebra 2 students, I gave them a list of exponent rules.

We wrote a word summary of what type of problem each exponent rule would help us with.  My marker choice was not good for photographing...  Sorry!


They were really struggling with applying these to the problems we were simplifying.  They kept claiming that they just didn't know where to start.

Eventually, I broke down and gave them an order of steps to follow.  This helped them a lot.  Though, I wish they could solve these problems without me writing out step by step directions.


We were working on simplifying expressions like this:

I guess where I struggle with this is that it *should* be review in Algebra 2.  We don't have time to derive all of the rules from scratch.  But, they act like they've never seen anything like this before.  My main motivation for doing this as a skill is to prepare for dealing with negative and zero exponents when we work with rational exponents and logarithms.

I also drilled into their heads that (2xy)^2 = 4x^2y^2.  For the past few years, most students have said 2x^2y^2 which was driving me bonkers.  We did lots and lots of practice problems with that, and I don't think I've seen anyone make that mistake at all lately.  Yay!

If anyone has ideas about how to review this without reteaching it from the beginning, I'd LOVE to hear it!

Exponent Rules file is here.
↧
Search

Solving Equations using the Three Essential Rules of Math Foldable

October 6, 2015, 5:30 am
$
0
0
When reviewing solving equations in Algebra 2, I borrowed Glenn's Three Essential Rules of Math.

I typed them up as a foldable to reduce the amount of writing my kiddos had to do.  Here's the outside:


And, examples on the inside:


We did a few practice problems.  I made them draw in the 1's and 0's that they made, but I guess I forgot to do it when I wrote out my own solutions in my notebook.  Oops...

And, for the record, we did more than 3 practice problems.  But, I only copied down three.


I can't decide how well I like this method.  The ones and zeros didn't help my students as much as I'd hoped.  I think if they were taught this way from the beginning, it might work much better.  Once they get to Algebra 2, they seem pretty set in their equation solving ways whether they are doing it correctly or incorrectly.  

Download the file here!  The font is HVD Comic Serif Pro.  
↧
↧

Reviewing Integer Operations + Order of Operations in Algebra 2

October 6, 2015, 5:30 am
$
0
0
My Algebra 2 classes were participants in my action research project over remediating integer operations.  I blogged about that more here.  Based on what group students were randomly assigned to, they received a certain set of notes.

Group 1:


Group 2:




This second group of students used a number line and bingo chip to work out the questions.


Then, we took notes over the Order of Operations.  I re-sized my order of operations hop scotch this year.  Link to download files is at the bottom of the post, as always.

Usually, I find that students don't really listen to reviewing the order of operations because they are convinced that they already know how to do it.  After all, they've been doing the order of operations since third grade or so.

To (hopefully) get their attention, I told them that I was going to tell them how their third grade teacher got the order of operations wrong.  We were going to Algebra 2-itize the order of operations.  Of course, a student told me Algebra 2-itize wasn't a word.  #sad


Here's the Cliff Notes version:

Parentheses - Your third grade teacher taught you that you should always work out the parentheses first.  He or she should have taught you that grouping symbols always need to be done first.  These could be parentheses.  They could be fancy brackets.  Did you know that there are invisible parentheses around the numerator and denominator of every fraction???  [Later, I decided I should have also said that there are invisible parentheses inside any radical!]  We should cut your third grade teacher a bit of slack, though, because when you were at that age, the only grouping symbols you ever saw were parentheses.

Exponents - Your third grade teacher taught you that exponents should always come next in the order of operations.  This year in Algebra 2, we're going to learn a cool way to rewrite any radical symbol as an exponent that is a fraction.  This means that radicals (or roots) have to be done during the exponent stage of the order of operations.

Multiplication and Division from Left to Right - This one is pretty self-explanatory.  Except, students have to be reminded of the left to right aspect.  Many students admitted that they had a teacher tell them that they ALWAYS have to do all the multiplication before the division.  And, I believe this.  It's one of the things about PEMDAS that drives me crazy.  

Addition and Subtraction from Left to Right - Again, I emphasized the left to right aspect.

Then, I threw this problem up on the board:



I asked, "What does the Order of Operations say we should do first?" Half of the class was convinced that we do 4(5) first.  The other half of the class said we needed to take care of the exponent.  This led to a discussion of another way our third grade teachers misled us.  When we were taught to always do parentheses first, parentheses were only ever used as grouping symbols.  We were still using the x to mean multiply.  It wasn't until we got to middle school that we really started using parentheses to mean multiplication.

I made them write a note about how when we see parentheses in a problem, we need to check and see if they are grouping parentheses or multiplication parentheses.

We did a few practice problems together in our notebooks.  Here's a few:



Foldables and graphic organizers can be downloaded here.
↧

Emphasizing Polynomial Vocabulary

October 7, 2015, 5:45 am
$
0
0
Polynomials are one of my favorite algebra topics to teach.  It's the type of topic that sounds scary.  But, I love getting to show students just how un-scary these problems can be.  Every year, my explanations are getting clearer, and I'm more in tune to what students are going to find frustrating.  This year, we're flying through polynomials in Algebra 2 really quickly.  Things seem to be clicking after the first explanation.  Yay!

Here's what things look like this year:

A polynomial frayer model.  I gave students the top two boxes.  They had to come up with examples and non-examples as a class.  Next year, I want to add a polynomial/not a polynomial card sort.


Next up: Parts of a Polynomial

In the past, I've always jumped straight from definition of a polynomial to naming polynomials.  And, my kids have always struggled.  This year, I decided to add in two intermediate steps.  This added an extra day, but I think it's already paid for itself by speeding up things as we move along through the unit.

I made a poof booklet to explain how to identify the different parts of a polynomial.  Then, we did two examples together.  Students later did a few more examples on their own.


I felt like the cover of our poof book was a bit lacking.  Next year, I'm totes going to add some cute clip art.


Students were asked to underline the terms and highlight the coefficients.


Then, they circled the constant if it existed.  They rewrote the leading term below.


Then, they identified the leading coefficient and the degree of the polynomial.  We were only dealing with single-variable polynomials.  I didn't teach them to find the degree of x^2y^2 - xy + 5.

Only one student noticed my missing "L" in "LABEL." I didn't even notice it.  Sad day...  I hate when I make typos.


Things I liked about this: students weren't confusing degree and number of terms.  This re-emphasized that terms take the sign in front of them.  This will be important throughout the year.  It was another chance to practice spotting invisible numbers.  I made them write in the invisible coefficients.  It helped set us up for our discussion of standard form!

Students did an entire quiz (only 2 questions, but still...) over labeling the parts of a polynomial.

On the same day as the polynomial frayer model + parts of a polynomial, we also did standard form.  


All of a sudden, the phrase "leading term" made sense.  Yay!


I used this to fit in distributive property and combining like terms practice.  My Algebra 2 students are still struggling a bit with combining like terms.


Then, naming polynomials.  Since I had already covered the parts of a polynomial on the previous day, I made a new naming polynomials graphic organizer.


We did naming polynomials speed dating.  I still had my set of cards from last year.  This was one of the activities featured in the audio of my NPR story.    

Here's an example of two of the cards:


Each student gets a card.  One side has a polynomial written on it in marker.  The other side has the name of the polynomial written in pencil.  Students stand up and pair up.

The goal of speed dating is to get to know something about the other person as fast as possible and to exchange information in case you later decide you want to get to know them better.  The goal of this activity is to figure out the name of the other person's polynomial as fast as possible, to exchange information (trade cards), and find a new partner to get more practice.

In this example, one player would tell the other that he/she was a linear monomial.  If correct, the person congratulates them.  If incorrect, he or she is to be coached by the person holding the card.  Repeat for the quartic polynomial.  Trade cards.  Repeat with another person.

It's fast-paced, it's loud, it's fun.  It's full of math talk.  It's everything I want an activity to be in my classroom.

Here's the front of some of the cards:


And the backs:


Naming polynomials went so much smoother this year!  Spending a day on vocab really, really helped my kids gain confidence.  

I already posted about factoring the GCF out of polynomials here.  

Up next will be adding/subtracting polynomials, multiplying polynomials, dividing polynomials, and factoring polynomials.  So much fun still to be had! 

Downloadable Files:

Parts of a Polynomial

Standard Form

Naming Polynomials
↧

Adding and Subtracting Polynomials Notes

October 8, 2015, 5:30 am
$
0
0
Here are my adding and subtracting polynomial notes from Algebra 2.

Nothing super exciting here.  I mainly did this to emphasize the importance of always using parentheses and what it means to distribute a negative.  Kids always seem to make mistakes with both.  This is a specific skill that is tested in Algebra 1 in Oklahoma at the moment.

My Algebra 2 students are really struggling with the idea of combining like terms this year.  Next year, I need to make this a skill to review before our polynomial chapter!


Fill in the blank notes.  (For the record, I didn't get this typed and printed in time, so my students had to hand-write the 5 steps.  But, I went ahead and typed it out so I would have it for next year.)  


Just the steps:


Example 1:


Example 2:


In the past, I've done this activity with my students to practice this, but I decided to skip it this year.

Download the file here.
↧
↧

Logic Puzzle Love: Masyu Puzzles

October 9, 2015, 5:30 am
$
0
0
I tried out some Masyu puzzles the other day with a group of students.  These are a new-to-me puzzle that I learned about from Jeffrey Wanko.

Usually, I'm drawn to logic puzzles involving numbers.  (I've posted about KenKen, Futoshiki, Hashi, Shikaku, and Paint by Number puzzles before.)  But, these have no numbers involved.  Actually, there are no words or numbers involved.  Here's how Dr. Wanko describes them:  


I found a packet he had created online that walked students step-by-step through discovering the rules of the game on their own.


I showed this to my students, and they derived some of the rules on their own.  But, I had to show them the actual rules before we could attempt to play:


I'm not going to lie.  A bunch of my kids got confused and gave up.  But, a few stuck it out with me.  They persevered and eventually figured a few puzzles out!  I also found these puzzles super challenging at first.  It took me quite a while to come up with a solution strategy.  I think this is a good thing, though.  I need to be reminded on a daily basis how it feels to struggle with learning something because that's how students feel every day in my classroom.

Want to try these out with your students?  I'd recommend using these free (PDF) pre-planned packets that are found here and here.  Or, maybe you're in the mood for something different.  Give them a try yourself!  Just don't blame me if you get frustrated!  :)  
↧

Harry Potter Quote Poster

October 10, 2015, 5:30 am
$
0
0
The other day, Casey tweeted a request for a poster.  In an attempt to procrastinate on my to-do list, I gave it an attempt.  It's a Harry Potter quote, and I'm not a Harry Potter fan.  I'm pretty sure I read part of the first book when I was in middle school.  And, I've been in a room with someone watching the movies, but it's just not my thing.  (Please don't stop reading my blog over this confession.  Thanks.)

I did, however, see the appeal of the quote: "You will find that help will always be given at Hogwarts to those who ask for it."
It's something I struggle with as a teacher.  Why, oh why, do my struggling students not ask for help???  When there are twenty-odd students in a classroom, vying for my attention, the students who ask for help are the ones that get it.

In a funny turn of events, Meg had already uploaded a pretty, colored poster version of this quote here.  You can download my less colorful version (pictured above) here.  
↧

Multiplying Polynomials Using the Box Method

October 11, 2015, 6:56 am
$
0
0
I finally got to introduce my Algebra 2 students to the box method.  I've been waiting impatiently for this since August.  I used the box method last year with my Algebra 2 students to multiply and divide polynomials.  Some of them are taking pre-calculus this year, and they came back to tell me that they had taught the method to some of their classmates!  As soon as I heard how excited they were about having done that, it just made me really excited to teach this year's group of students the magic that is the BOX.

I typed out the notes.  This is a first.  Usually, I just show my students how to do it.  But, I do recognize the importance of them having something to look back on if they forget the process.


This was a first attempt at writing out the steps.  I'm sure these will morph and grow over the years like the rest of my notes do!


Then, we did some practice problems together.


I had them note the degree of each polynomial to see if it has any 0 terms in it that need to be taken into account.  At the multiplying stage, you can leave out the zeros, and everything will work just fine.  But, the like terms won't always be on the diagonals.  Plus, having the zeros is essential when using the box method to divide.  So, I want my students to get in the habit of including the zeros now.
I think the moment when my students really started buying into this method was when we color-coded the diagonals and saw the like terms.  If all the terms in a diagonal are not like terms, we know we made a mistake somewhere!

One student raised his hand to say he liked this method a lot better than the way a previous teacher taught him with drawing arrows all over the place.  That's the way I was taught, and it worked just fine for me.  But I've seen students forget to distribute a term to every other term so many times.  Drawing the boxes (if drawn correctly) shows students just how many times they have to multiply.


They often get frustrated trying to figure out where the zero rows/columns go.  But, they definitely get a sense of satisfaction when they get to fill in that whole row or column with zeros!  


Here's what the problems end up looking like when we work them out on the SMART Board.  My boxes were a bit wonky, and it definitely showed when I used the highlighter tool...  


Download the file for this page here.
↧
Search

A Daily Problem

October 12, 2015, 5:54 am
$
0
0
One of the first strategies I picked up as a student teacher was to write the date as a math problem.  I started doing this as a first year teacher.  My kids hated it.  It especially frustrated them when they would ask the date and I would read the math problem off the board to them.

Last Christmas or so, I got a bit overwhelmed one week and never made the time to write the date on the board.  And, I just kinda stopped.  I didn't mean to; I just got out of the habit.



Well, I'm back at it.  And, my students are not pleased.  I couldn't be happier!

The date in the picture above sparked a great conversation about whether the 2+1 needed to be in parentheses.  I love when I can find extra little ways to make my students think!
↧
↧

5 Number Summary 5 Finger Summary

October 13, 2015, 5:29 am
$
0
0
Let's take a moment to reminisce.  There aren't a ton of things I remember from first grade.  I remember my teacher's name was Mrs. Charboneau.  That was hard to spell as a first grader!  We colored teddy bears on the first day of school.  One of our assignments for the year was to count to 100 for our teacher.  And, my favorite math worksheets were the ones that said 2 + box = 5.

I also remember getting back worksheets about reading the time from a clock that were covered in red ink.  Analog clocks and I didn't get along for the longest of times.  That all changed when my parents bought me my first watch.  It had 5, 10, 15, 20, etc written around the circumference.  I was super proud of that watch, and I actually still have it.  Now that I think of it, that's kinda weird...  

You know what else I remember?  If we finished early with an assignment, we were supposed to turn it over and draw a picture while we waited for our classmates to finish.  Now, I'm not the most artistic of people.  But, I can trace.  So, my usual go-to was to trace my hand and decorate it with rings and pretty fingernails.

The other day in stats, I had my students trace their hands to make a summary of five number summaries.  One of my students has a broken arm, so we had to have someone else trace their hand on his paper.  I was really confused when he told me he couldn't do the assignment.  Then, when I realized what he meant, I felt really bad.    


And, for the record, my ring finger isn't deformed.  @theshauncarter just decided to, you know, put a ring on it.  I didn't have this problem in the first grade, so I didn't really think about it until I'd already started...
↧

Stats Card Sort: Reporting IQR vs. Standard Deviation

October 14, 2015, 6:51 am
$
0
0
My stats students had just finished up learning to find IQR by hand and by calculator and standard deviation by hand (I know - I'm evil!) and by calculator.  It was now time to discuss when each is more appropriate to report.  I quickly decided to make a card sort for my students to complete.


I don't think I can post the file since the images are taken from Stats Modeling the World.

And, if I'm honest, I'm not entirely sure I have them sorted perfectly.  Teaching stats definitely puts me outside my comfort zone.  Anything that's not algebra is outside of my comfort zone.  This is my fourth year teaching algebra 5 out of 6 periods a day.  Algebra and I are good friends.  Stats is just a visitor that stops in for an hour a day every other year.  We've still got a long way to go to become well acquainted!  


It was awesome to eavesdrop on my students' conversations as they worked to sort these graphs.  I have a special place in my heart for card sorts.  <3
↧

Knocking their SOCS off in stats

October 15, 2015, 5:30 am
$
0
0
First of all, sorry that I'm posting all my stats stuff in a random order.  I've got so many notebook pages to post, so I've just been doing whichever pages are easier to post.  Maybe at some point I'll make a blog page to put them all in order.

So, for today's post, we're talking about identifying the shape, outliers, center, and spread of a quantitative variable.    I stole the SOCS idea from @druinok.  Let's face it.  I steal most of my stats ideas from her.  She's been an absolute lifesaver this year!

I typed up a quick foldable to give my students to keep in their interactive notebooks.  My stats students are the slowest writers in the world.  I learned this the hard way.  So, I've been typing everything I can for them.  


Shape:


Outliers:


Center:


Spread:


All of the inside:


To practice describing SOCS, I had my class look at this dotplot of the Kentucky Derby Winning Times between 1875 and 2008.  We had quite the interesting discussion about why the data was shaped this way.

I took this graph from Stats: Modeling the World.


Then, I took a few practice problems out of our textbook (Stats: Modeling the World) and made them into a quick foldable.  Since we only have stats every other year, the school doesn't have textbooks.  I have one copy of the book that I use as a reference.  



Here are the files for this lesson.
↧

The Geometry of Tangrams

October 16, 2015, 5:30 am
$
0
0


Guys, I currently have more drafts sitting in blogger than there are days in the school year.  This. Is. Not. Cool.  Can I just take a year off from teaching so I can catch up on blogging?  Just kidding.  Then, there'd be no things teenagers say, and life would be sad.

A few months back, I took a master's course on Conceptual Geometry.  One of our assignments was to write a story that could be used in our classroom and to illustrate it with tangrams.  Some of my classmates e-mailed our professor and complained that this was a very elementary task and not applicable to the secondary teachers enrolled in the course.  

As a result, we were given a different assignment based on Grandfather Tang's Story: A Tale Told With Tangrams by Ann Tompert.  I really enjoyed working through the lesson, so I made a note to write a blog post to 1) share it with you guys and 2) be able to find the lesson again if I ever teach geometry!  


I was excited for a reason to pull out my class set of tangrams that I bought a while back from Amazon.  I've only ever used them in a brain teasery way in my classroom, but working through this activity showed me their potential to be used in the geometry classroom.


This is one of those activities that makes me say, "Man!  I wish I taught geometry!"

My favorite activity from the lessons was this one:



So much beautiful mathematical thinking required.  You can find the entire activity here on UKY's site.  The lesson goes on to explore area perimeter of the tangram pieces and designs in several different thought-provoking ways.  If you teach geometry, I'd definitely suggest checking it out!

↧
↧

Students Notice!

October 17, 2015, 5:30 am
$
0
0
A student drew this flower on her integer quiz.  I thought it was cute, so I snapped a picture of it using my phone before handing it back.  When I handed back her quiz, she asked me if I'd noticed the pretty picture she had drawn me.


I was able to say I did.  In fact, I even took a picture of it.  She thought this was very cool.  Students notice when we notice them and their efforts.  We're nine weeks into the school year, and I still feel like I don't know all of my students on a personal level.  Some of them are still just a name, a face, and a score in the grade book.  I definitely need to work on this.  
↧

Prime Climb Game and an Interesting Problem

October 18, 2015, 5:30 am
$
0
0
At my last math teachers' circle meeting, we played a new-to-me game: Prime Climb.


This game has one of the most beautiful, math-y game boards I've ever seen.


Now, I can't really talk about the actual game all that much because we didn't play by the actual rules.  In the actual game, players have two pawns.  We used one.  In the actual game, there are action cards.  We didn't use these at all.

Here's how we did play:

Place your pawn on START.

Roll two ten-sided dice. (0-9)  

Add, subtract, multiply, or divide the value of each die to your current place on the board.  For example, if I'm on START and roll a 3 and 7, I can add 3 and add 7 to end on 10, add 3 and multiply by 7 to end on 21, add 7 and multiply by 3 to end on 21, or add 7 and subtract 3 to end on 4.

You cannot go past 101.  You must apply the operations to the dice separately. And, if you land on the same number as another pawn, you send that piece back to start.

The first player to land on 101 wins.

As a roomful of math teachers, we loved the mental math aspect of this game.  My group didn't really want to be vicious and send others back to start, but I think my students would have zero problems with that!

After we played a round, our facilitator challenged us to list every single space on the game board that we could be on and in one roll end up winning.  Now, that was a fun problem to solve!  We got a lot of mileage out of this seemingly simple problem.  Especially because our answer was different than our facilitator's answer.  Then, she gave us 12-sided dice (1-12) to see how that changed our answer.  All in all, very interesting!  

From these past few math teacher circles, I've discovered that while I'm not usually the fastest at solving problems in the group or the best at seeing unique ways of solving a problem, I do bring something to the group.  I'm really good at organizing information and illustrating the problem.  When I'm presented with a new problem, it takes me a while to process it.  My first instinct is to pause and process the problem, then I try to come up with a way to organize the information I have.  Only then, do I try to solve the problem.

Last month, with the lunes and balloons spherical geometry problem, this meant drawing the problem on a balloon.  My groupmates were easily solving the first few problems while I was still trying to wrap my mind around what we were doing.  However, as the problems became harder, they started using my physical representation to solve the problems.

With this Prime Climb problem, my first instinct was to draw a hundred chart to organize which numbers were one step away from winning and which numbers were more than one step away from winning.  Drawing a grid and writing out the numbers 1-100 was time consuming.  And, it seemed like my group was rushing ahead of me.  But, I persevered at creating my visual representation.  Once I started marking the numbers on my chart, my groupmates were all using my hundred chart to help come up with the next solutions.  In the end, everyone was copying from my chart to their notes.  

Maybe this is why I'm so drawn to interactive notebooks.  I love organizing information.  I'm not the fastest at math.  I'm not the best.  I'm not the cleverest.  But, I am really good at visually organizing information.

So, has anyone played with the actual rules?  I'm trying to decide if this is a game I wan to invest in for my classroom.  The reviews on Amazon are all really good, but most mention playing with young children.      
↧
Search

Translating Words Into Symbols Coloring Notes

October 19, 2015, 5:18 am
$
0
0
One of our Algebra 1 standards is that students be able to translate between written expressions and equations and symbolic expressions and equations.  This is one of those topics that drives me crazy to try to teach because it seems so intuitive to me.  My students, however, have traditionally struggled with it.

If I ask them to translate "the sum of a number and five," they can usually come up with "x + 5." No problem.  But if I ask them to translate, "the product of a number and the sum of the number and five," they shut down.

I know there's a lot of talk in the MTBoS about not teaching kids which words mean which operation.  And, I see where they are coming from with this.  Half of can mean multiply by 1/2 or divide by 2.  Per can mean multiply or divide.  But, if students don't know what the word quotient means, how am I supposed to help them without giving them a chart???

Here's this year's attempt at teaching this topic.  


In the past, I've had students make foldables and list the key words.  This was time consuming, and I often found myself giving students a lot of the words because they couldn't come up with them on their own.

Here's a pic of a foldable from a couple of years ago:


I knew I wanted to try something new this year.  I thought about doing a card sort to glue in, but a million little pieces to glue in and my Algebra 1 students don't mix well.  Then, I remembered how @druinok had modified a statistics card sort I had made to be a coloring activity.


I decided to make a coloring page for my students to complete.


The kids kept trying to classify the words that mean equals as add/subtract/multiply/divide which was frustrating.  We did this as a class.  I asked them to suggest words for addition.  We colored all those.  Then, subtraction, etc.

We drew arrows over the "turn around words." This wasn't enough, however, to make it stick for my students.  This needs some more work for next year!  

I think I'll keep the coloring aspect for next year.  I missed some phrases when putting this together quite hastily.  (Read: during first hour plan to teach third period!)  So, I definitely want to try and make it more comprehensive.

I also want to come up with a way to signify that some words can mean multiple different operations.  Still working out the best way to do that.  Any suggestions on improving this lesson would be greatly appreciated!

Another area my kids have struggled with in the past was knowing when to use parentheses.  I decided to try a new approach this year.  

I had students draw ovals around all of the operation words.  Then, I had them draw a rectangle around the equation/inequality word, if applicable.  If there are 2+ ovals on one side of the rectangle, I told them they needed to use parentheses.

Now, you and I both know that these parentheses are sometimes redundant.  But, I'd rather my students putting parentheses and not needing them than needing them and not putting them.


Practice Problems:


Note to self for next year: TYPE THESE!


A common question type my students struggle with is writing expressions that match a scenario that builds on itself.  I put one of these on the quiz, and it was still the most missed question.  I think my mistake was not giving students independent practice with this question type.  That's another thing to fix for next year!


Download files here!

↧

Converting Units Interactive Notebook Page

October 20, 2015, 5:30 am
$
0
0


This year, I decided to make converting units into a review skill in Algebra 1.  I'm not sure if I'll do this again.  My main goal was to get students thinking about units.  But, I feel like this lesson may have just added to the confusion of my students.

Here's the notes we did on Day 1 of this skill:


I bolded the conversion factors that let us switch between the metric system and the imperial system.  Then, I also gave students a chart to use to switch between prefixes within the metric system.



They were super duper confused by this chart.  I had them draw a giant 1 on the left hand side of the chart.  We read it as "1 kilo(meter) equals 1000 meters." "1 centimeter equals 0.01 meters." It seemed clear as day to me, but my students still struggled.  Note to self: find a better way to explain this next year!

I also ran into students thinking that each conversion factor had to be applied in order.  For example, they thought if we had feet that we *had* to convert to yards.

Inside, we did 5 practice problems using the fence post method that I learned in high school chemistry.  Set up your conversion factors so the units cancel out.  Multiply all the numerators.  Divide by all the denominators.  Presto.  You have an answer.

Kids asked why this worked.  I showed them that multiplying by 365 days and dividing by 1 year is the same as multiplying by 1.  All we were doing is changing our units.


If I were going to do this again, I would spend a day on just simple conversions and spend a separate day on converting things like m/s to mph.  We saved that problem until last, but it was just too much in one day for my kiddos.

The next day in class, we did some Australia inspired practice problems.

14,896 km - The distance I traveled to Australia this summer.  One student asked if I measured the distance in my car...
When Shaun was in America last winter, he commented about how high some of our speed limits were.  I decided to make this into a problem as well.  



Next, we talked about the price of stuff in Australia.  We had to convert from liters to gallons AND Australian dollars to US dollars.  Some of my kids were shocked that Australia had their own form of currency.  I promised to show them some Australian money IF they got busy on this problem.


This led to kids proclaiming how expensive things were in Australia which led to a discussion of how much money Australians make.


Comparing the American minimum wage to the Australian minimum wage was a real eye-opener for my students.  

It was fun to share a bit of my summer experiences with my students and show them a real-world application of what we were learning. 

Download file here. 
↧
↧

Come Explore the MTBoS

October 20, 2015, 3:54 pm
$
0
0
Hi guys!

I know this makes two posts in one day, but I'm just too excited to wait until tomorrow to post this.  So, you'll just have to excuse this blogging faux pas.

I know I talk about the MTBoS a lot here on this blog.  And, I realize that most of you fall in one of a few categories.

1.  I love participating in the MTBoS by tweeting and/or blogging.
2.  I love participating in the MTBoS by reading blog posts and leaving comments.
3.  I don't know what the MTBoS is, but I enjoy reading math teacher blogs.



If you're in Category 1, I hope that you've already heard about the upcoming MTBoS Exploration and have signed up to be a mentor.  Or, if you feel like you're still getting your feet wet in the MTBoS, you can sign up to be given a mentor.  A mentor's job is to help people get acquainted with the MTBoS and answer any questions people might have about getting involved in blogging or twitter.



If you're in Category 2 or 3, I want to encourage you to join in by starting a blog or twitter account.  We're really a friendly bunch of math teachers.  And, we'd love to have you join us!

The sign up form is here for both mentors and mentees.  Mentees will be paired up with mentors in December, and there will be a 4-week blogging initiation that starts in January.  Get all the info here!

If you've ever thought about blogging before but have been scared off by the idea, here's your chance to join in with a whole group of people doing the same thing at the same time with tons of support.
↧

Using Equations to Solve Word Problems

October 21, 2015, 5:30 am
$
0
0
I'm determined to incorporate more word problems into my Algebra 1 course throughout the year instead of saving them until we review for the EOI exam at the end of the year.  I decided the best way to do this was *gasp* turn it into a skill that students need to demonstrate mastery of.

I put together this quick booklet foldable with practice word problems in it.  The questions are taken from released EOI questions from the Oklahoma State Department of Education.  I'm not sure if this will actually be of use to anyone else, but I thought I'd go ahead and post it.

Download a copy of this file here.

Outside:


Inside:


Close-Ups:





↧

Graphing Ordered Pairs in Algebra 1

October 22, 2015, 5:30 am
$
0
0
I ended up using the same graphic organizer for graphing ordered pairs in Algebra 1 as I did in Algebra 2.  I tweaked things a tiny bit, so I thought I'd go ahead and post again.  In the past, I've pulled out the shower curtain coordinate plane and practice graphing on that with my Algebra 1 students, but I just feel soooooooooo far behind this year.  This is a topic they should have mastered in middle school.

Tweaks:

* Only put quadrant numbers in the circles
* Made note of what to do if the x or y value is 0

Note for next year: make this into a booklet foldable with practice problems inside!  Ask students to label ordered pairs.  Ask students to draw and label ordered pairs that meet certain requirements.


And, my new and improved kangaroo that I actually remembered to graph all the points on.


Download files here. 

↧
Viewing all 1077 articles
Browse latest View live
Search